Siddharth Saha | Paper Review: OctoMap - 3D mapping framework based on octrees

This paper¹ attempts to efficiently build a probabilistic 3D occupancy map using the octree data structure

The key characteristics that contribute to the efficiency of OctoMap are noted below:

Volumetric Model It implements an occupancy grid mapping approach based on an octree.

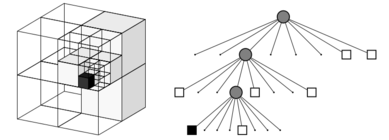
Fig 1: Octree storing free (shaded white), occupied (shaded black) and unexplored (dots) cells
Probabilistic Sensor Fusion Model
$P(n|z_{1:t})$ represents the probability of leaf node $n$ to be occupied given sensor measurements $z_{1:t}$
\[P(n\|z_{1:t}) = \left[1 + \frac{1-P(n\|z_t)}{P(n\|z_t)} \frac{1-P(n\|z_{1:t-1})}{P(n\|z_{1:t-1})} \frac{P(n)}{1-P(n)} \right]^{-1}\]
We introduce the log-odds notation and assume a uniform prior $P(n) = 0.5$
\[L(n) = log\left(\frac{P(n)}{1-P(n)}\right)\]
This allows us to simplify the update equation as follows
\[L(n\|z_{1:t}) = L(n\|z_{1:t-1}) + L(n\|z_{t})\]
Clamping the Update Policy This enables the map to adapt to dynamic changes in the environment.
\[L(n\|z_{1:t}) = max( min(L(n\|z_{1:t-1})+L(n\|z_t), l_{max}), l_{min})\]
Tree pruning
If all the children of an inner node of the octree are known to be have the same occupancy probability, the children are pruned. This is lossless as the parent still contains the occupancy probability value. Tree pruning carried out recursively drastically reduces memory utilisation and speeds up map updates.